[NLP] Transformer 모델 분석 (Self-Attention)

현재 Attention is All you Need는 NLP를 한다면 반드시 읽어야 될 논문일 뿐만 아니라 인공지능을 연구한다면 반드시 읽어봐야 할 논문이 되었다. 꽤 오래 전에 읽고 정리해놓은 내용을 기억을 상기시킬 겸 포스팅한다. 이미 수많은 블로그에서 자세히 포스팅되어있으니 요약본 느낌으로 간단히 설명하고자 한다. 거의 모든 그림 및 내용은 http://jalammar.github.io/illustrated-transformer/ 을 참고하였다. 추가적으로 NLP의 다른 기본 내용을 좀 더 쉽게 이해하고자 한다면 이 글을 읽어보는 것을 추천한다.

Overview

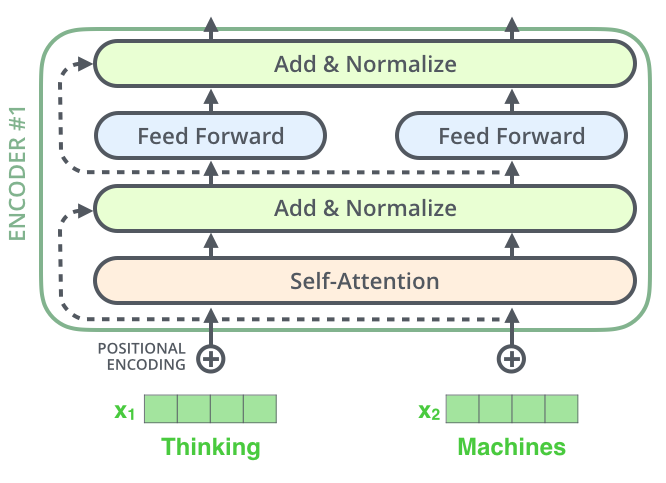
해당 논문에서 나오는 Transformer 모델을 high-level에서 먼저 살펴보자. 일단 다음과 같은 Encoder-decoder 구조를 지닌다.

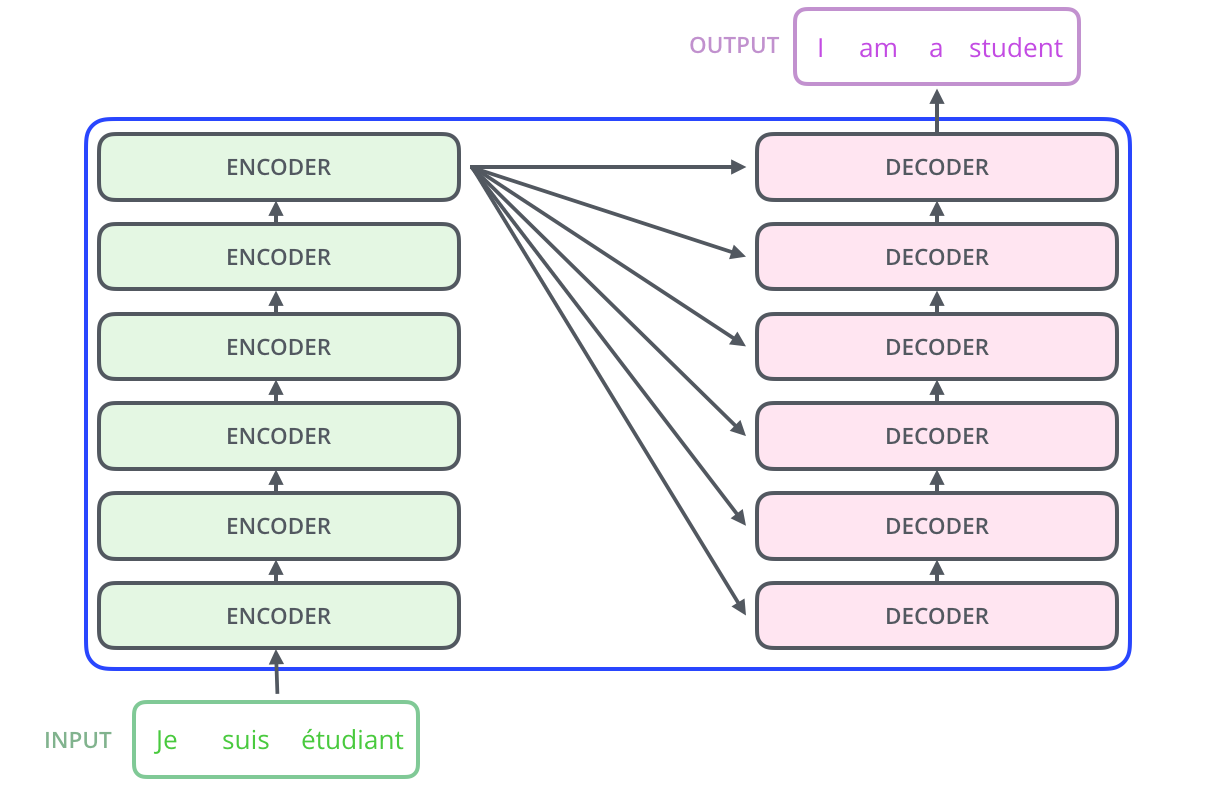
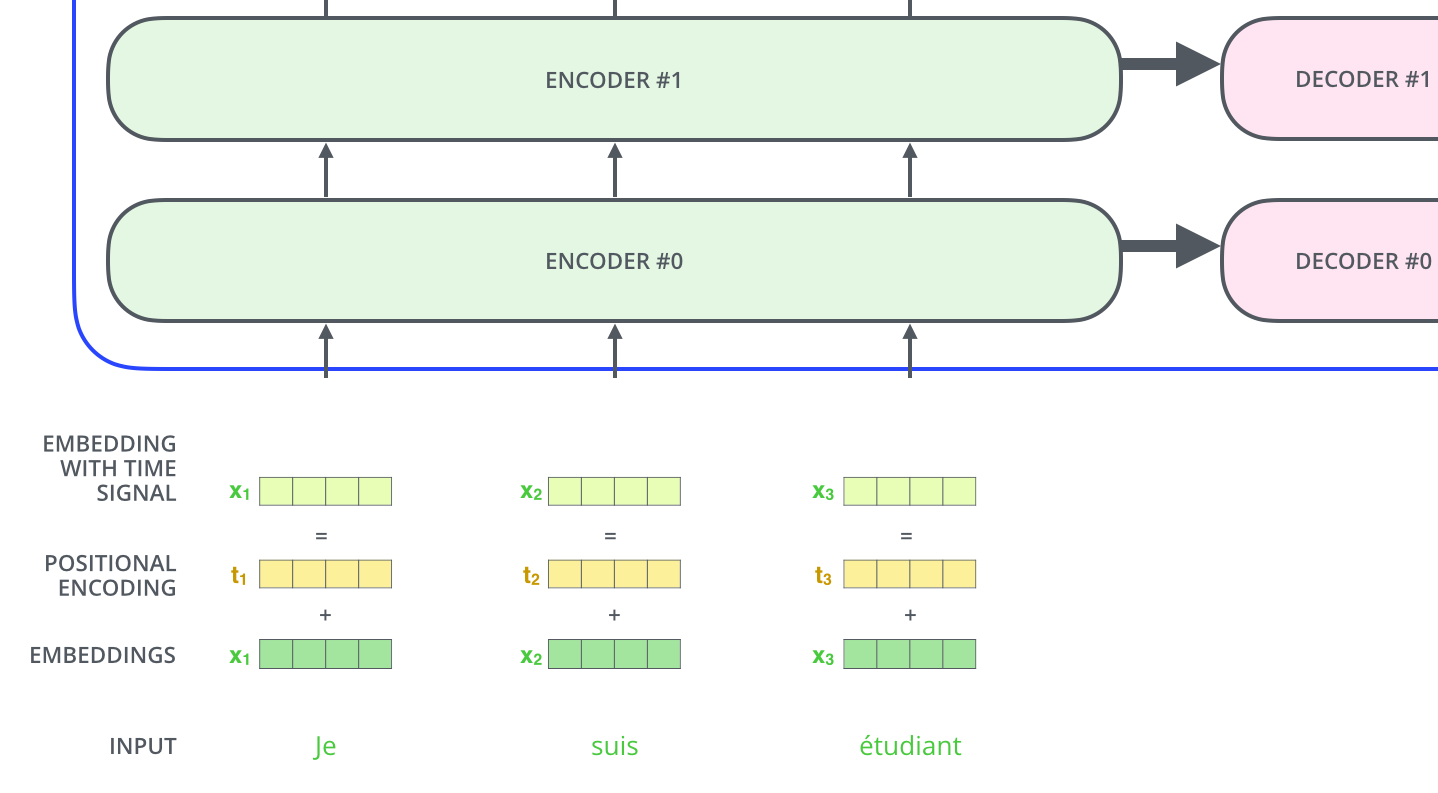
Transformer 모델은 6개의 encoders와 6개의 decoders로 이루어져 있으며, 각각 동일한 구조이며 독립적인 모듈로써 존재한다. 위 그림에서 보다시피 입력은 encoder에 의해 임베딩되고, 임베딩된 context는 각각의 decoder에 입력으로 들어간다.

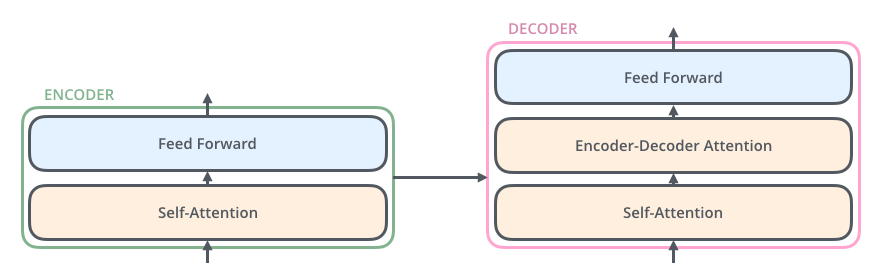
각각의 모듈을 좀 더 자세히 살펴보자. Encoder는 self-attention 레이어와 feed forward 레이어를 통해 context를 임베딩하고, decoder는 이전 decoder의 출력과 encoder의 출력을 입력으로 받아 세 개의 레이어를 통과하여 decoding한다.

여기서 Self-Attention 모듈은 말 그대로 자기 자신의 attention을 계산한다. 예를 들면, 영어 단어에서 it이라는 대명사는 독립적으로는 절대 정확한 내용을 알 수 없다. 그렇기에 문장 내 다른 단어들을 참고하여 그 의미를 해석해내야한다. 이를 위해 Self-Attention은 특정 feature가 같은 context 내에서 어떤 features를 참조하고 있는지 attention을 계산한다.

Encoder-Decoder Attention은 기존 seq2seq 모델에서 사용된 attention과 비슷하다. 여기서는 입력 시퀀스의 적절한 부분에 집중하도록 도와주는 역할을 한다. 잠시 기존 attention을 수식으로 설명해보겠다. 입력 $x=(x_1,...,x_{T_x})$, 출력 $y=(y_1,...,y_{T_y})$이면, encoder의 hidden state $h_t=Encoder(x_t)$이라 하고 decoder의 hidden state $s_i=Decoder(s_{i-1},y_{i-1},c_i)$다. 여기서 attention scoring을 하는 방법은 논문마다 다르니 매커니즘만 참고바란다. 이전 decoder의 출력 $s_{i-1}$과 encoder의 hidden states를 입력으로 모든 encoder hidden state 각각에 대해 energy $e_{ij}=a(s_{i-1},h_j)$, ($j$는 encoder의 hidden state의 time step)를 계산한다. 이를 가중치 0~1로 환산하기 위해 softmax를 거치면 attention $\alpha_{ij}=exp(e_{ij})/\sum^{T_x}_{k=1}exp(e_{ik})$가 계산되고, encoder hidden state와 weighted sum하면 context vector $c_i=\sum^{T_x}_{j=1}\alpha_{ij}h_j$가 최종적으로 계산된다. 이를 수식으로만 깔끔하게 정리하면 다음과 같다.

$input\ x=(x_1,...,x_{T_x}),\ \ output\ y=(y_1,...,y_{T_y})$
$h_t=Encoder(x_t),\ \ s_i=Decoder(s_{i-1},y_{i-1},c_i)$
$e_{ij}=a(s_{i-1},h_j)$
$\alpha_{ij}=exp(e_{ij})/\sum^{T_x}_{k=1}exp(e_{ik})$
$c_i=\sum^{T_x}_{j=1}\alpha_{ij}h_j$

이렇게 계산된 Attention은 다음 그림과 같이 decoding할 때 어떤 embedded features에 집중할지 도와준다.

Encoder

위에서 설명했듯 각 Encoder는 Self-Attention 레이어와 feed forward 레이어를 가진다.

Self-Attention

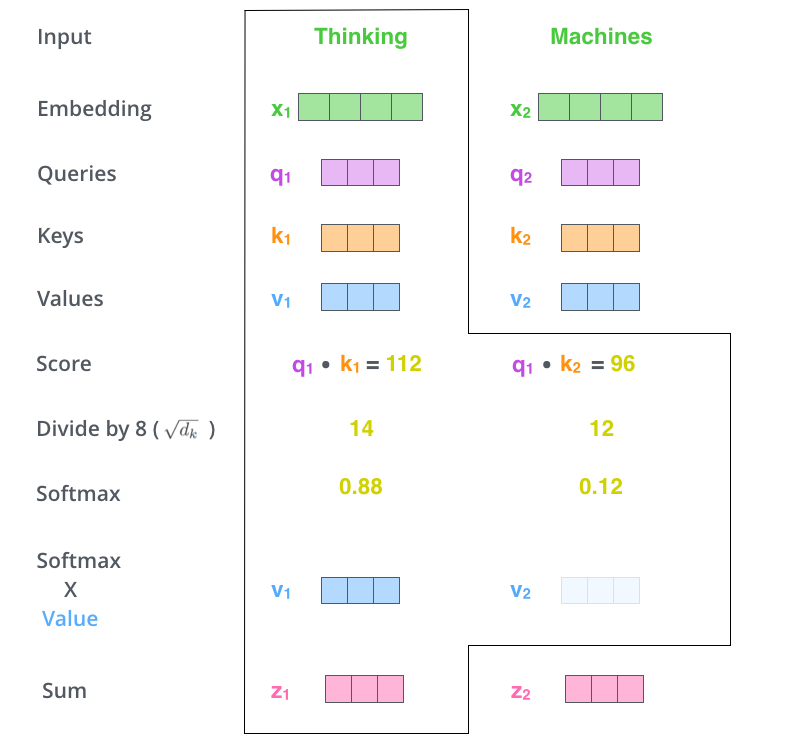
Step 1) 각 input vector로부터 세 벡터를 만든다.

세 벡터는 Queries, Keys, Values로, 각각 trainable weights $W_Q,W_K,W_V$와 입력 단어를 임베딩한 $x$와 곱하여 생성된다.

Step 2) 특정 위치의 단어가 다른 단어와 얼마나 연관되어 있는지 점수를 매긴다.

Query 벡터와 Key 벡터를 dot product하여 계산된다. 위 그림에서 보듯 $i$번째 단어와 $j$번째 단어 간의 연관 점수는 $q_i\cdot k_j$를 통해 계산된다.

Step 3) 계산된 점수를 Key 벡터의 차원 수의 제곱근으로 나누어준 뒤 Softmax를 취한다.

수식으로 나타내면 $Softmax({{QK^T}\over {\sqrt{d_k}}})$와 같다. 차원 수의 제곱근으로 나누어주는 이유는 dimension이 클수록 score 값 자체가 매우 커지고 (결국은 곱한 뒤 모든 원소를 합하므로) 이에 Softmax를 취하면, total sum이 크기 때문에 값들이 매우 작아지고 gradient 소실 문제가 발생하기 때문이다.

Step 4) Value vector에 softmax score를 곱한다.

$Attention(Q,K,V)=Softmax({{QK^T}\over {\sqrt{d_k}}})V$

이를 그림으로 나타내면 다음과 같다.

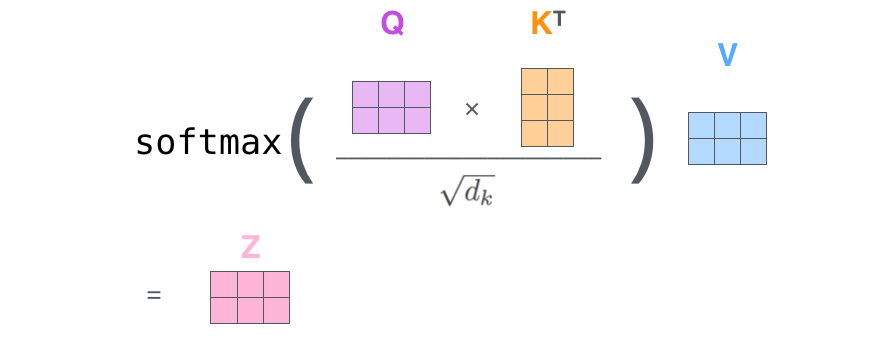
논문에서는 이 Self-Attention layer를 Multi-headed attention layer로 재정의했다. 아래는 encoder의 전체적인 연산이다.

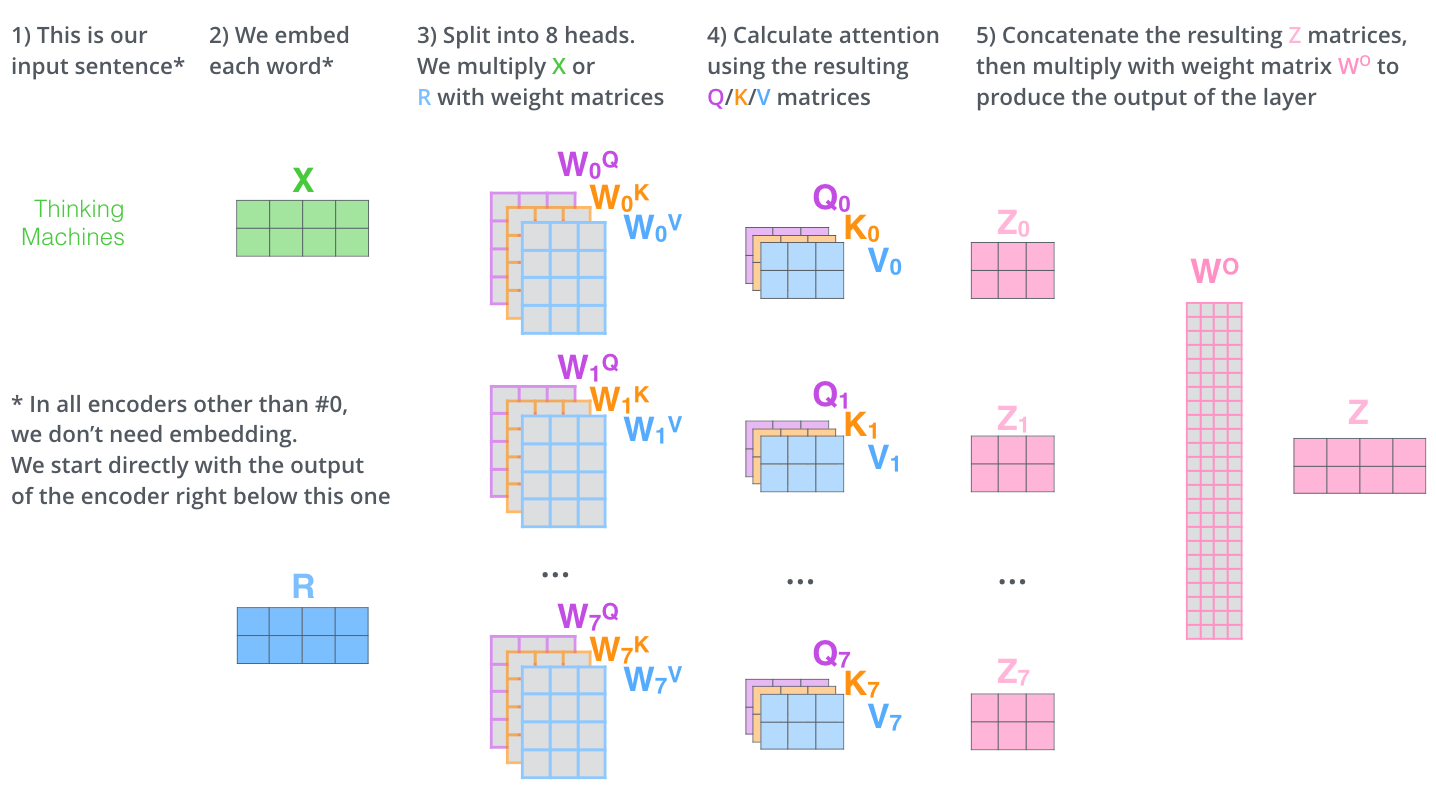
첫 번째 encoder 이외에 다른 encoders는 임베딩이 필요하지 않고 바로 아래에 있는 encoder의 출력 R을 사용한다. 결국 여러 개의 self-attention 레이어가 동일한 입력 하나에 대해 연산된다고 보면 된다. 각각의 출력 Z는 concatenation 후 feed forwarding 되어 하나의 Z 벡터를 출력한다. 사실 보면 알겠지만, 모든 heads는 병렬적으로 연산이 가능하다.

그렇다면 위 Attention layer를 일반 Attention layer와 비교했을 때 장점은 무엇일까?

1) 다른 위치에 집중할 수 있도록 한다. 일반 attention layer는 위 attention matrix를 보다시피 자기 자신에 크게 영향을 받는다. 그러나 예를 들어 'it'이 어떤 것을 참조하는지 알아야 할 때는 좋지 못하다.

2) 다수의 representation subspace를 지닌다. 이건 multi-head로 정의하기 때문에 생긴 장점인데 다수의 Query / Key / Value weights가 존재하기 때문에 각기 다른 부분 공간을 나타낼 수 있고 이에 따라 embedding space가 한정적으로 되는 것을 막는다고 생각할 수 있다.

Input Embedding

위에서 계속 설명했듯 입력 시퀀스는 벡터로 embedding 되어 모델에 입력된다. 기존 embedding 방법은 단어 간의 순서를 고려하지 않았었는데 Transformer 모델은 position embedding을 추가함으로써 모델이 시퀀스 내 다른 단어들 간의 거리 혹은 위치들을 결정하도록 학습시킨다. 좀 더 직관적으로 보면, position embedding을 추가한 것이 Q/K/V 벡터에 project되고 dot-product attention이 되면 임베딩 벡터 간 의미 있는 거리를 제공한다고 볼 수 있다.

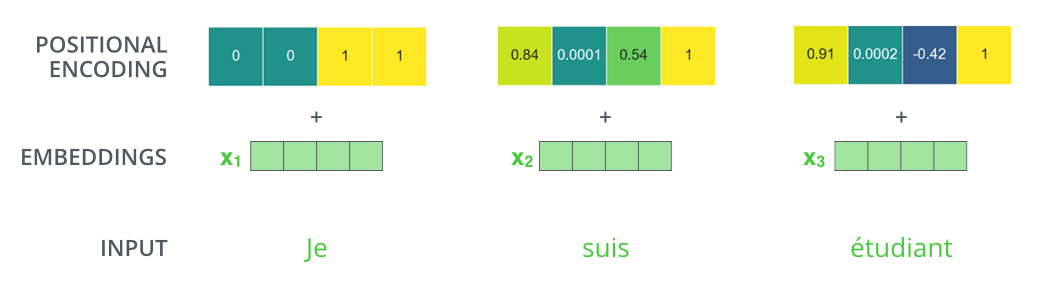
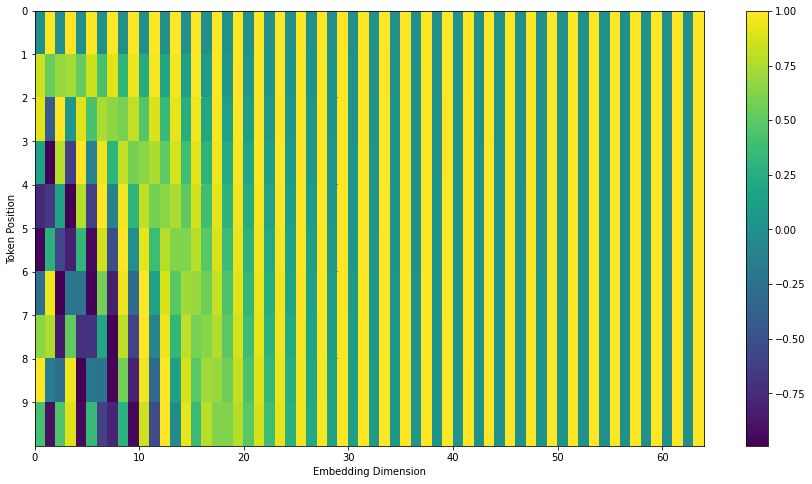
각 vector의 원소 값의 범위는 -1~1이고 구하는 코드는 다음과 같다.

get_timing_signal_id()

xxxxxxxxxx
input sequence 길이 = length, 임베딩 차원 수 = channels
position = [start_index ~ start_index+length-1]
num_timescales = channels // 2
log_timescale_increment = log(max_timescale/min_timescale) / (num_timescales-1)
inv_timescales = min_timescales*exp([0~num_timescales-1]*(-log_timescale_increment))
scaled_time = position*inv_timescales
signal = concat([sin(scaled_time), cos(scaled_time)], axis=1)
signal = pad(signal, padding=[[0,0],[0,channels%2]])
signal = reshape(signal, shape=[1,length,channels])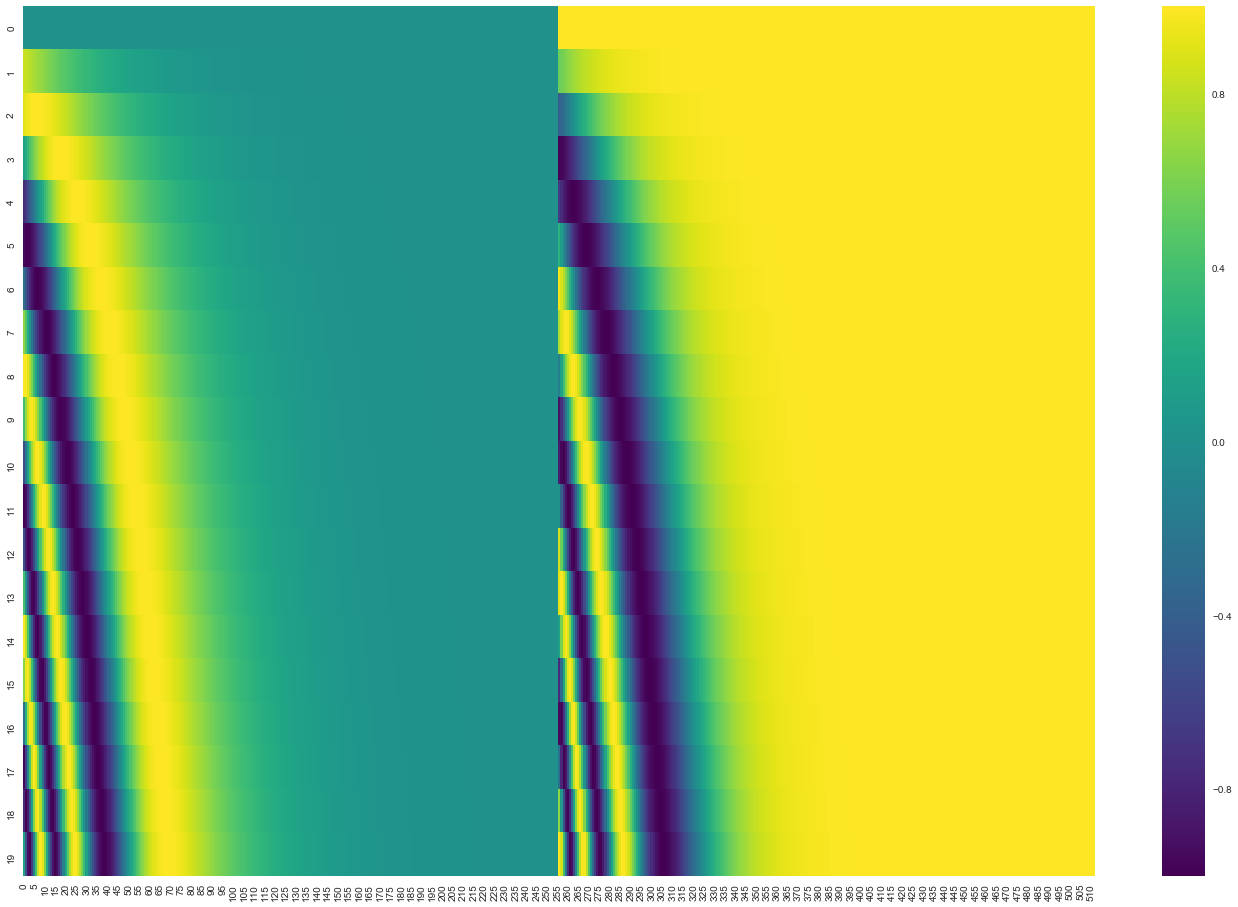

위 그림은 임베딩 차원 수가 512인 20개의 단어에 대한 position encoding이다. 왼쪽은 sin 함수에 의해 생성된 것이고 오른쪽은 cos 함수에 의해 생성된 것이다. 이 둘을 concat하여 사용한다. 또 다른 방식으로는 논문과 약간 다르게 바로 concat하지 않고 interweave 하는 방식도 있다. 그렇게 하면 아래와 같이 encoding 된다. 참고

The Residuals

참고 글에서 그림으로 너무나도 잘 나타내주셨기에 다음 그림들만으로도 충분히 세부사항을 파악할 수 있다.

위에 점선으로 나타낸 것이 residual connection이다. 여기선 concat하지 않고 더해주었다.

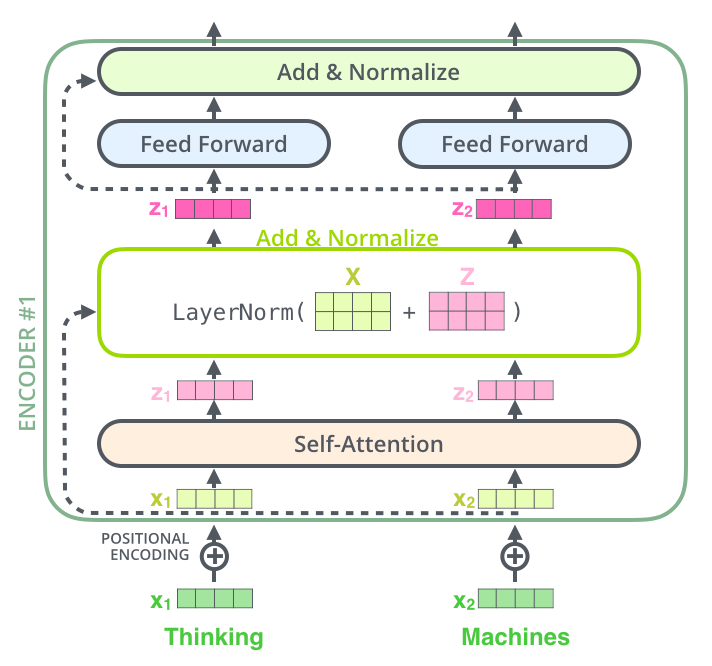
추가적으로 batch size에 종속적인 batch normalization 대신 layer normalization을 사용하였다. [참고]

전체적으로 보면 다음과 같다.

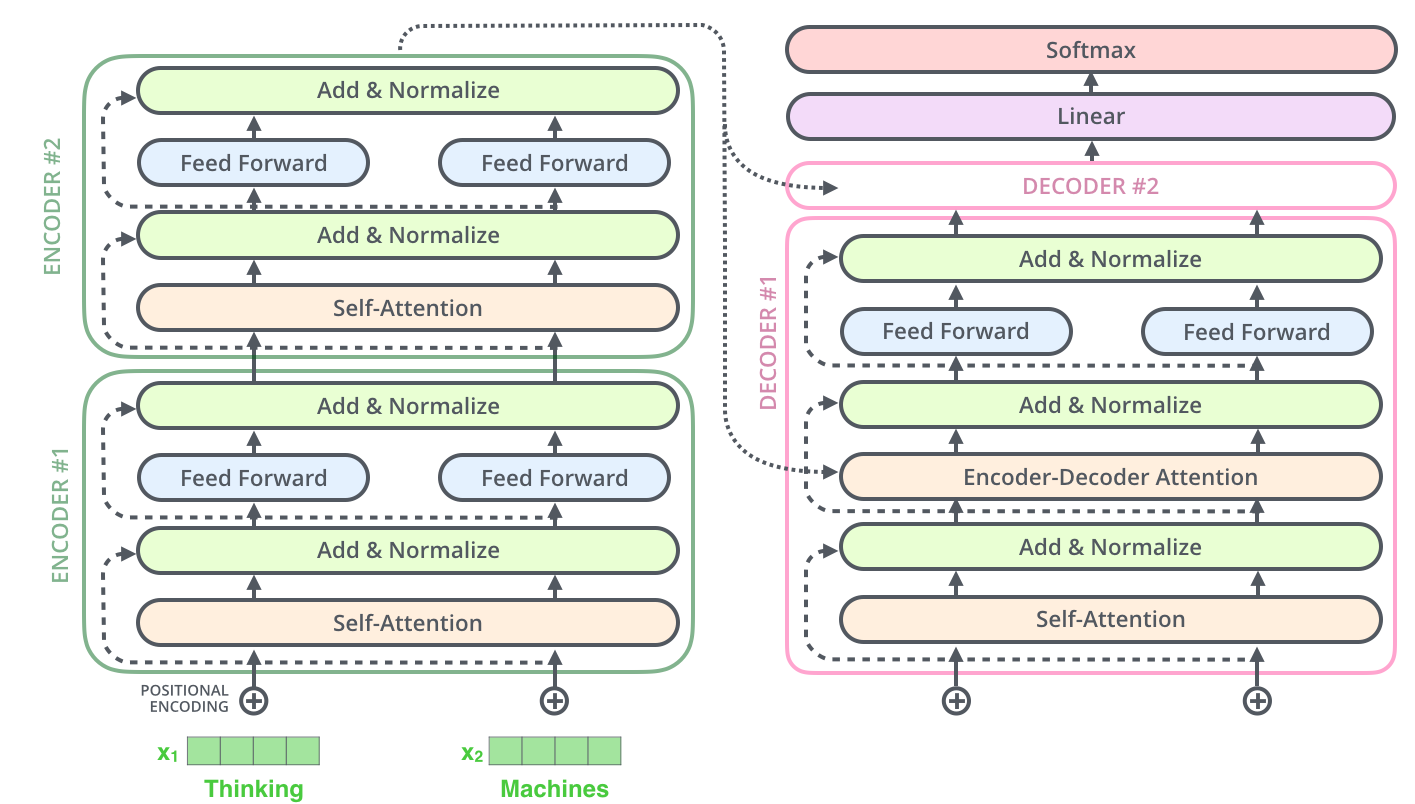
최종적으로 Stacked encoders의 마지막 출력은 각 decoder에 forward된다. 어떻게 forward 되는지는 decoder 부분에서 설명하겠다.

Decoder

Encoder의 최종 출력은 attention vectors K와 V로 변형되고 각 decoder의 encoder-decoder attention layer에서 사용된다. Decoder가 입력 시퀀스의 적절한 위치에 집중하도록 돕는 것인데 위에서 설명된 기존 seq2seq attention에서 encoder의 hidden states라고 생각하면 된다.

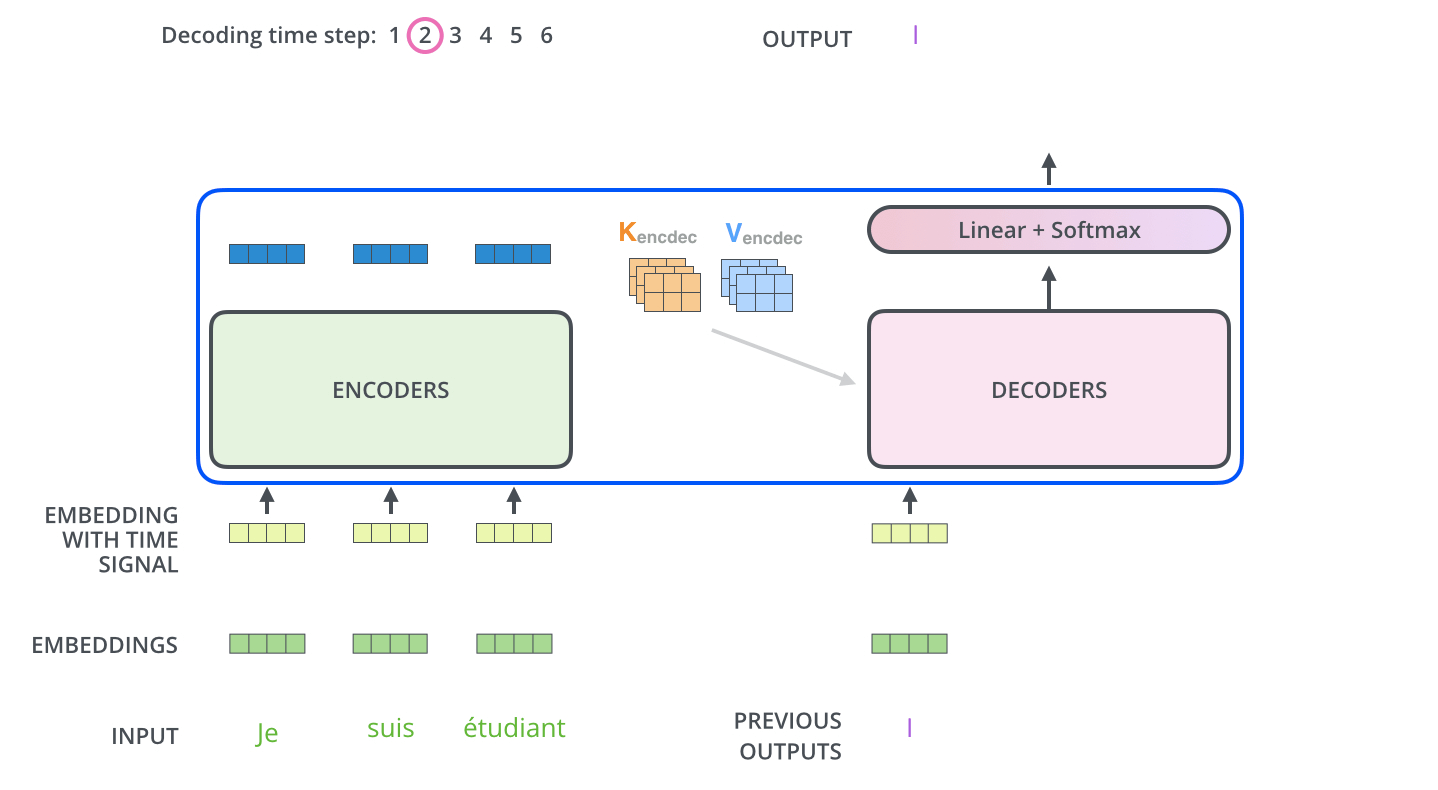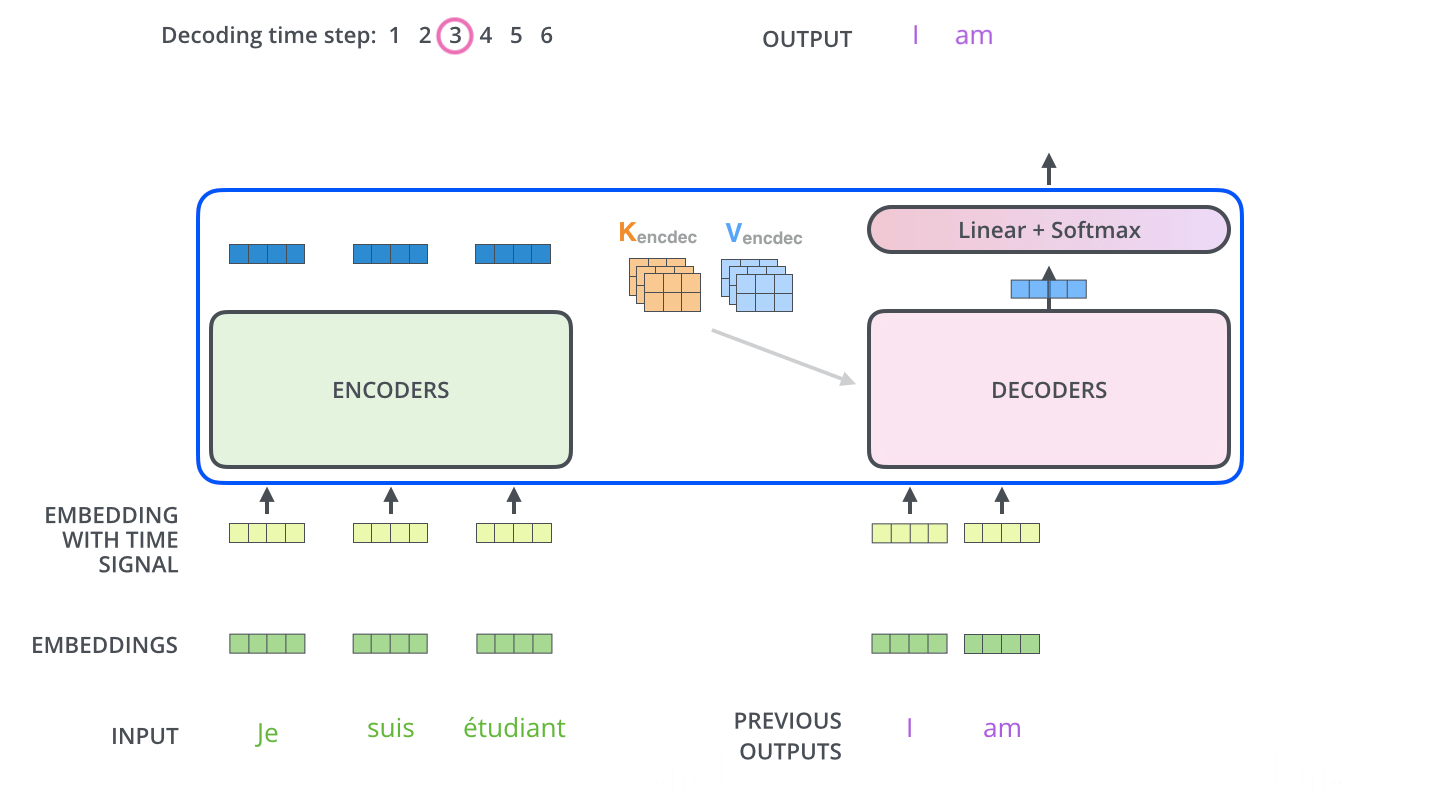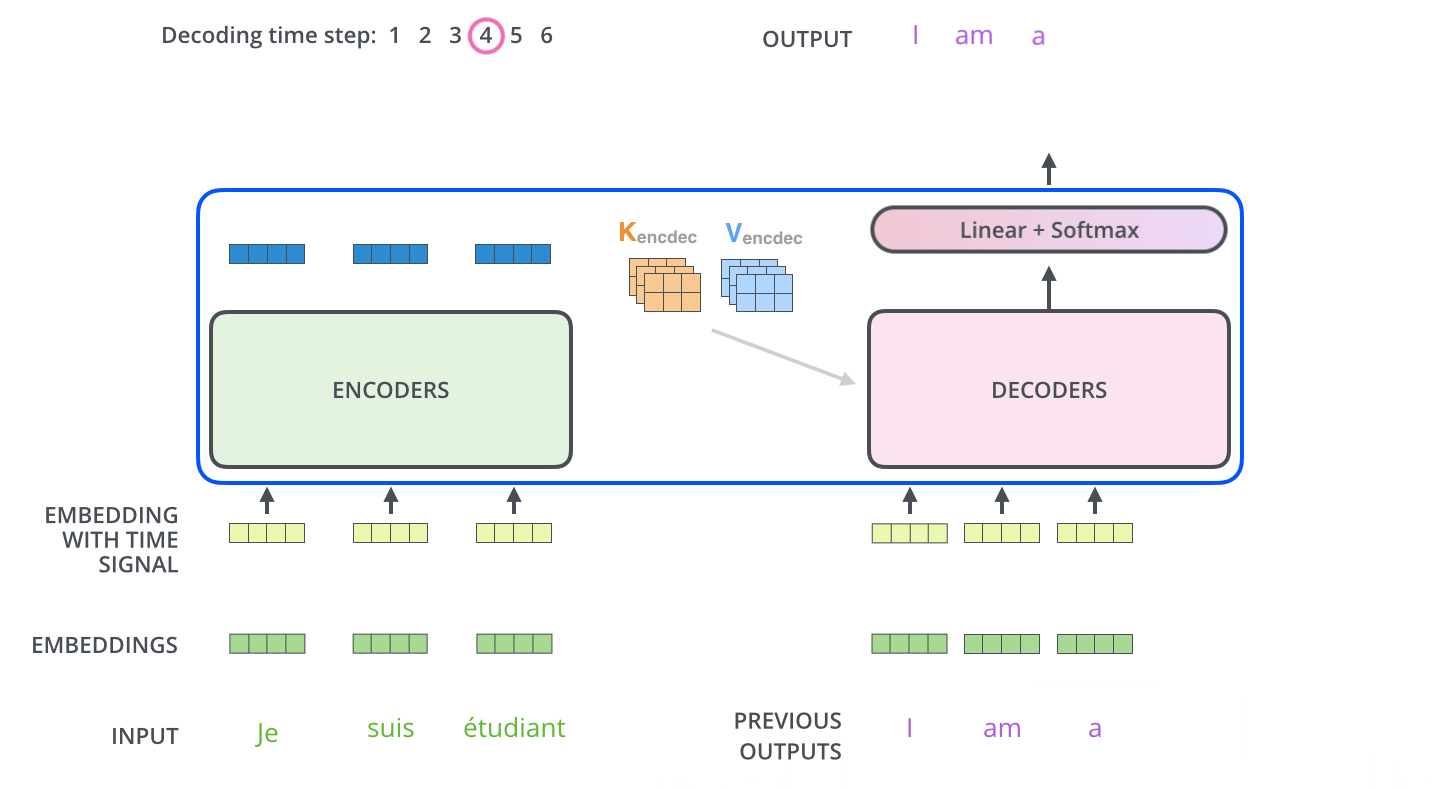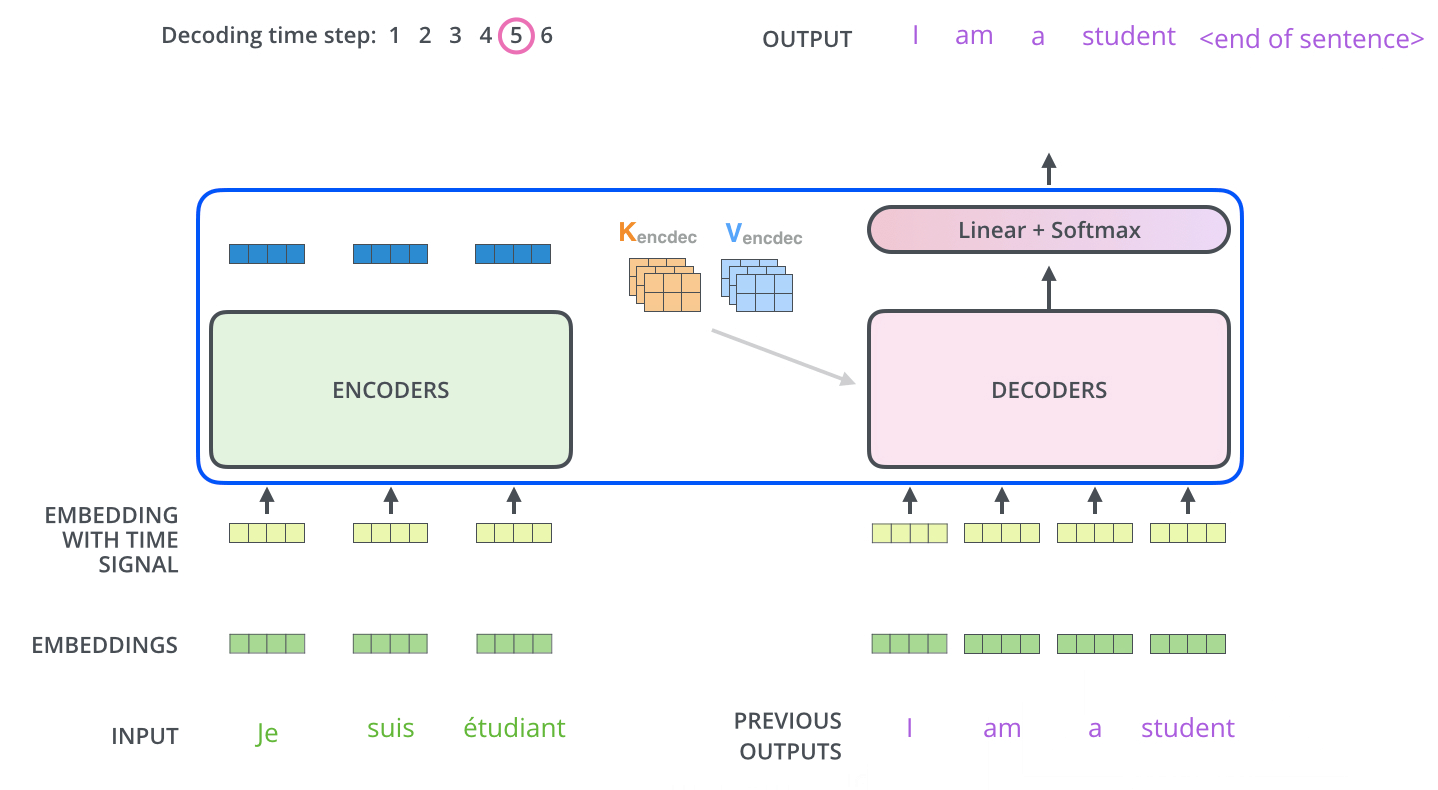
결론적으로 decoder는 이전 step의 decoder 출력을 입력으로 받고 decoder가 이를 linear + softmax를 거쳐 단어로 decoding 하게 된다.

내부적으로 좀 더 살펴보면, decoder에서 self-attention 레이어는 encoder와는 약간 다른 방식으로 연산한다. Encoder는 하나의 시퀀스를 차례로 입력받을 필요없이 한꺼번에 입력받아 embedding 할 수 있고 이 때문에 병렬 처리가 가능하다. 하지만 decoder는 순차적으로 결과를 생성해내야 하기 때문에 병렬적으로 처리할 수가 없는데 이를 해결하고자 마스킹을 하여 attention을 진행한다. 즉, 아직 다음 출력이 나오지 않은 상황이기 때문에 그 자리는 -inf와 같이 마스킹하여 이전 출력에만 attention을 주면 병렬 처리가 가능해지기 때문이다.

그 다음 encoder-decoder attention은 Query 벡터는 decoder로부터, Key / Value 벡터는 encoder로부터 가져와 연산을 진행한다. 위에서 이야기한 것처럼 encoder의 hidden states는 K, V, decoder의 hidden states는 Q가 되어 연산된다.

이 포스트는 모델 구조와 내부 연산만을 다루었으며, loss와 같은 다른 세부사항은 다른 블로그의 포스팅을 참고하는 것이 좋을 듯 하다.